Computation of Heat and Fluid Flow using Spectral Methods

Previous Next

Numerical resolution of fluid flows and heat transfer is essential for comprehensive characterization and optimization of thermal systems. Over the years, several methods like finite difference (FDM), finite volume (FVM) and finite element (FEM) have been developed, but their accuracy is limited due to their local nature.

In this work, we formulated high accuracy Chebyshev spectral methods and implemented domain decomposition for computational optimization. Spectral methods are widely used for resolving the base flow field in high fidelity stability analysis of fluid flows and for direct numerical simulation (DNS) of turbulent flows.

The spatial discretization was carried out using the Chebyshev collocation method, with a second order semi-implicit time integration scheme and projection method to handle the pressure-velocity coupling. Please refer to my thesis report for more specific details on the method, schemes and results. Here are some of the highlights from my thesis:

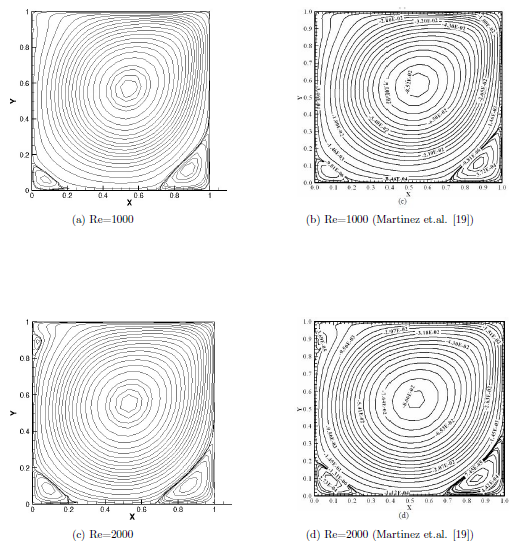
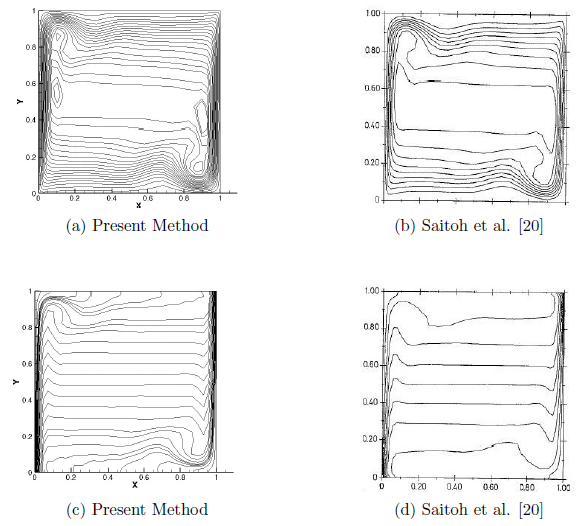
• Maximum deviation of 0.05% from benchmark results for a lid-driven square cavity problem and successfully validated the numerical algorithm for forced and natural convection.
• Implemented domain decomposition on heat conduction and channel flow problems with a maximum computational speed-up of 2.83 for four subdomains.